Coronavirus-Pandemie: Warum die Tests aus der Apotheke so gefährlich sind

Wer ist schon immun gegen Covid-19 und wer nicht? Antikörper-Schnelltests aus der Apotheke versprechen bequeme Gewissheit. Doch die Ergebnisse sind extrem unzuverlässig. Wir erklären, warum.

Wie viele Menschen sind oder waren mit dem Coronavirus infiziert? Das ist die große Unbekannte der Epidemie. In die offiziellen Statistiken fließen nur laborbestätigte Fälle ein. Forscher gehen aber davon aus, dass viele Infektionen mit milden Krankheitsverläufen unbemerkt bleiben.

Könnte es also sein, dass ein viel größerer Teil der Deutschen bereits an Covid-19 erkrankt und wieder genesen ist als bisher bekannt?

• Sonderseite: Zahlen und Statistiken zum Coronavirus

Antikörper-Schnelltests als schneller Ausweg aus der Krise

Sogenannte Antikörpertests sollen helfen, Licht ins Dunkel zu bringen. Sie können anhand Blutproben den Nachweis liefern, wie viele Menschen dem Virus bereits ausgesetzt waren und möglicherweise eine natürliche Immunität entwickelt haben.

In den USA werden die kommerziellen Tests diverser Hersteller bereits als schneller Ausweg aus der Corona-Krise propagiert. Wer positiv getestet wird – so die Idee –, wäre wahrscheinlich immun gegen das Virus, könnte zur Arbeit zurückkehren, sich um Covid-19-Patienten kümmern oder andere verantwortungsvolle Aufgaben übernehmen, die für andere derzeit zu riskant wären.

Doch die Antikörpertests sind bei Weitem nicht so zuverlässig, wie es den Anschein hat. Die Gefahr, dass viele Menschen fälschlicherweise positiv getestet werden und sich in Sicherheit wiegen, ist groß. Eine Beispielrechnung zeigt, warum das so ist.

Herstellerangaben führen in die Irre

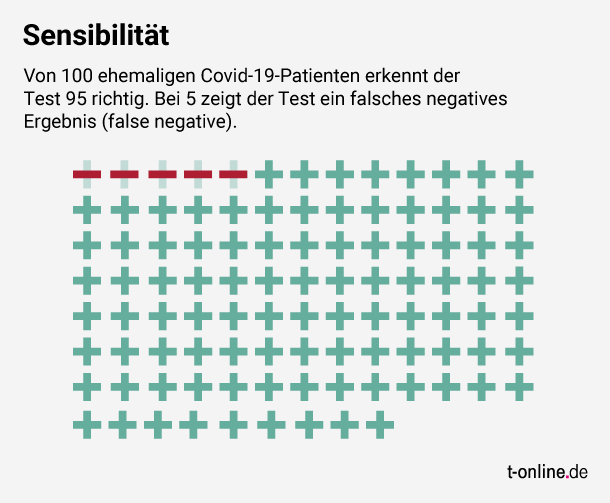
Laut Hersteller bieten manche Antikörpertests eine Sensibilität für SARS-CoV-2 von 95 Prozent. Das bedeutet, dass der Test von 100 Menschen, die die Infektion bereits hinter sich haben, 95 korrekt identifiziert. Bei 5 Personen zeigt der Test fälschlicherweise ein negatives Ergebnis (False Negatives). Diese Personen würden sich weiterhin schützen, die anderen zur Arbeit gehen und am Leben teilnehmen.

Doch was ist mit den Menschen, deren Körper noch keine Bekanntschaft mit dem Virus gemacht hat? Für die gibt es eine eigene Statistik.

Die Spezifität eines Tests gibt an, wie viele negative Fälle korrekt erkannt werden. Für diese Beispielrechnung nehmen wir eine Spezifität von 98 Prozent an. Das heißt: Von 100 Personen, die noch nie mit SARS-CoV-2 infiziert waren, erhalten 98 ein negatives Ergebnis – was der Wahrheit entspricht. Für 2 Personen zeigt der Test ein positives Ergebnis an (False Positives), obwohl es negativ sein sollte. Wenn diese Personen den Test für bare Münze nehmen und sich für immun halten, stellt das ein Risiko dar.

Wendet man den Test nun auf eine zufällige Stichprobe an, kommen solche False Positives weitaus häufiger vor. Bezogen auf ganz Deutschland würden bei den oben genannten Testeigenschaften sogar zwei von drei positiven Tests danebenliegen. Das hat damit zu tun, dass die Krankheit in der Bevölkerung noch nicht sehr weit verbreitet ist (Prävalenz).

Mit falschen Ergebnissen ist zu rechnen, nur mit wie vielen?

Derzeit muss man davon ausgehen, dass sich bisher weniger als 1 Prozent der Deutschen mit dem Virus infiziert hat. Für unsere Rechnung nehmen wir jetzt eine Gesamtbevölkerung von 10.000 Menschen an. Davon sind 1 Prozent, also 100 Personen immun. 9.900 sind es nicht. Aber wer gehört zu welcher Gruppe? Das wissen wir nicht. Das wollen wir ja mit dem Test herausfinden.

Gleichzeitig wissen wir aber schon zu Beginn des Tests, dass wir bei den 10.000 Resultaten mit einer gewissen Zahl an Fehlergebnissen (False Positives und False Negatives) rechnen müssen. Wie viele, verraten die statistischen Angaben des Herstellers zur Sensibilität und Spezifität des Tests.

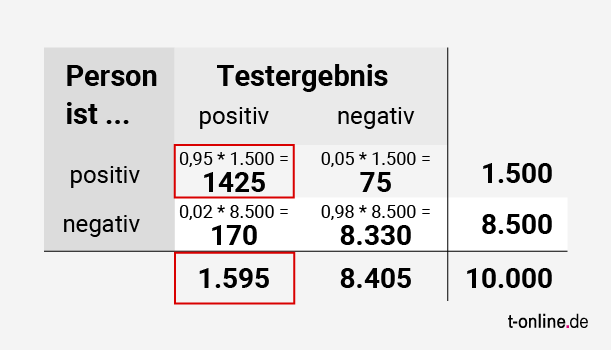
Um die Zahl der zu erwartenden Fehlresultate zu berechnen, nutzen wir eine Tabelle. In die tragen wir die unterschiedlichen Wahrscheinlichkeiten ein.

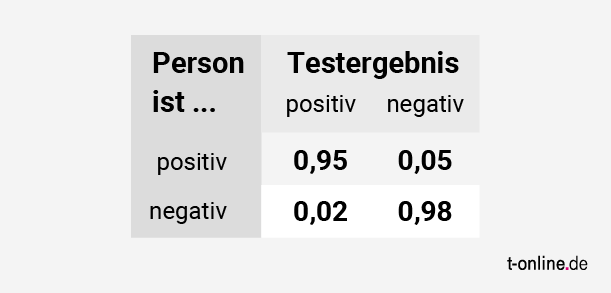
Die Wahrscheinlichkeit, dass eine Person, die positiv ist, auch positiv getestet wird, beträgt 95 Prozent (0,95). Die Wahrscheinlichkeit eines False Negatives beträgt 5 Prozent (0,05). Die Wahrscheinlichkeit, negativ getestet zu werden, wenn man negativ ist, beträgt 98 Prozent. Die False-Positive-Rate ist 2 Prozent.

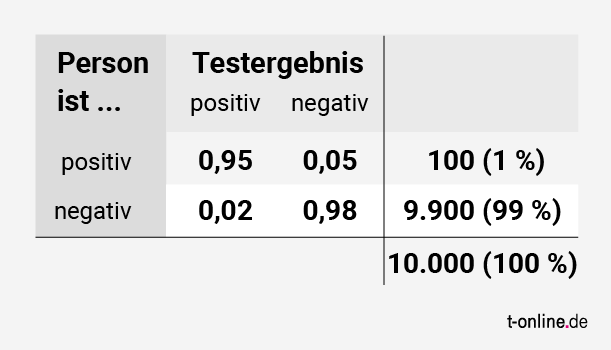
Ganz rechts unten tragen wir die Gesamtzahl der Personen ein, die wir testen wollen: 10.000. Statistisch gesehen ist oder war von diesen 10.000 Personen 1 Prozent tatsächlich infiziert. 9.900 hatten SARS-CoV-2 noch nicht. Das tragen wir in die Zeilen ein.

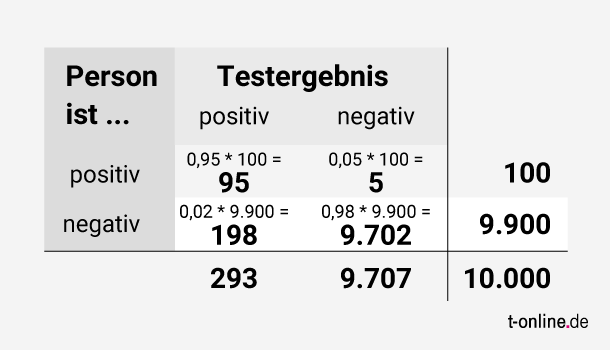
Jetzt können wir ausrechnen, wie viele Testergebnisse korrekterweise positiv oder negativ ausfallen und wie viele Fehlergebnisse es gibt.

Insgesamt fallen demnach 95 + 198 = 293 Tests positiv (3 Prozent) und 5 + 9.702 = 9.707 Tests negativ aus (97 Prozent).

Wie wahrscheinlich ist es jetzt, dass ein positives Testergebnis tatsächlich zutrifft? Das Verhältnis zwischen den tatsächlich Infizierten (True Positives) und der Gesamtzahl der positiven Tests verrät es: 95 / 293 = 0,32.

Auf jedes richtige Ergebnis kommen zwei Falsche

Die "wahre Trefferquote" des Schnelltests beträgt also nicht wie eingangs erwähnt 95 Prozent, sondern nur 32 Prozent. Nur ein Drittel der positiven Testergebnisse ist zutreffend und auf jedes richtige Ergebnis kommen zwei falsche. Die meisten kommerziell verfügbaren Tests haben sogar eine noch höhere False-Positive-Rate als in dieser Beispielrechnung angenommen.

Man kann natürlich einwenden, dass die miese Trefferquote nur temporär ist. Je mehr Menschen sich mit SARS-CoV-2 infizieren, desto zuverlässiger funktionieren die Schnelltests. Ein Beispiel: Im stark betroffenen Gangelt soll die Durchseuchung der Bevölkerung laut der Heinsberg-Studie bei fast 15 Prozent liegen.

Unter diesen Bedingungen würde unser Test die folgenden Ergebnisse liefern:

Das Verhältnis zwischen den positiv getesteten und tatsächlich Infizierten und allen positiven Tests beträgt 1425 / 1595 = 0,89. Auf einen positiven Test wäre demnach zu fast 90 Prozent Verlass, obwohl sich die Testeigenschaften nicht geändert haben.

Auf der Webseite des US-amerikanischen Sendernetzwerks NPR können Nutzer mit verschiedenen Werten herumspielen und herausfinden, unter welchen Umständen die Antikörper-Schnelltests mehr oder weniger aussagekräftig sind.

Eine Formel illustriert die zentrale Erkenntnis

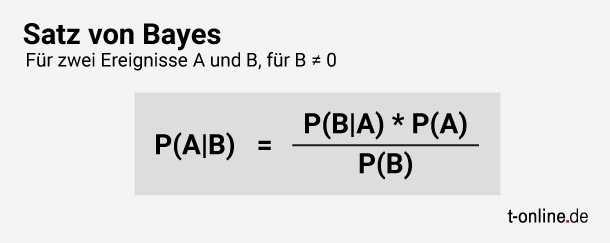
Statistiker berechnen solche bedingten Wahrscheinlichkeiten mit dem Satz von Bayes, benannt nach seinem Erfinder Thomas Bayes. Die Formel hierfür lautet:

Die P-Werte stehen dabei für die unterschiedlichen Wahrscheinlichkeiten, die wir zuvor in den Tabellen berechnet haben. P(B|A) entspricht dem Sensibilitätswert, den der Hersteller für seinen Test angibt.

Der Satz von Bayes illustriert eine wichtige Erkenntnis: Die Wahrscheinlichkeit, dass die Annahme A (Person ist positiv) zutrifft, wenn B gilt (Test ist positiv), ist nicht unbedingt gleich groß wie die Wahrscheinlichkeit, dass B eintritt (Test ist positiv), wenn A (Person ist positiv) gilt. Mathematisch ausgedrückt:

Fazit

Fakt ist, dass willkürlich durchgeführte Antikörper-Schnelltests für den Hausgebrauch zum gegenwärtigen Zeitpunkt sehr wenig Aussagekraft besitzen. Für medizinische Studien hingegen können die Schnelltests durchaus sinnvoll sein. Indem die Forscher die zu testende Grundgesamtheit eingrenzen, andere Indikatoren hinzuziehen und Gegentests durchführen, erhöht sich die Wahrscheinlichkeit, dass die Resultate stimmen.

Die Idee, dass ein positiver Schnelltest als "Persilschein" für die Teilnahme am öffentlichen Leben dienen kann, muss jedoch verworfen werden. Und das nebenbei bemerkt nicht nur aus statistischen Gründen. Denn ob man nach einer überstandenen Covid-19-Erkrankung nun immun ist oder nicht, ist immer noch nicht abschließend geklärt.